By Andy Horwood
Podiatric Innovations Ltd
Visiting Lecturer & Fellow Staffordshire University
Product Designer & Researcher at Healthy Step Ltd
Clinicians and therapists who manage locomotion dysfunction must understand biomechanical terminology to appreciate core concepts of tissue stress. What is presented here is a refresher. First, remember that quantities can be scalars or vectors. Scalars just have a quantity; examples being pressure or speed. Vectors also have quantity but require a direction to have meaning. Examples include force, moments, momentum, stress, and strain.
Force
This is a vector calculated by the mass of the object multiplied by the acceleration and it is Newton’s second law of motion. Acceleration is the change in velocity over time and velocity means displacement over time. Acceleration can be positive by increasing over time or negative by decreasing, such as when braking. A change in force over time is called an impulse. If you want to change a force, you must either alter mass or change the rate/direction of acceleration. This is why changing from heel strike running to forefoot running cannot reduce forces on the body. However, reducing the running pace or wearing lighter running shoes can.
Momentum
Momentum is mass multiplied by velocity. Even stationary objects have momentum, although moving an object gives it greater momentum. It is closely linked to Newton’s first law of inertia (an object’s motion cannot change without a force being applied) combined with his second law on force, save that acceleration is changed to velocity. Velocity is a vector that considers speed and direction together. Momentum indicates how hard or easy it will be to stop or start motion. The foot experiences the most dramatic changes in momentum within the body as it does not move its location during midstance, brakes hard at initially contact, and rapidly accelerates forward from heel lift to terminal swing.
There are two types of momentum: linear and angular. Linear momentum expresses events of an object moving from one location to another in a straight line, such as when considering a whole human moving over a 100m sprint. See Fig. 1.
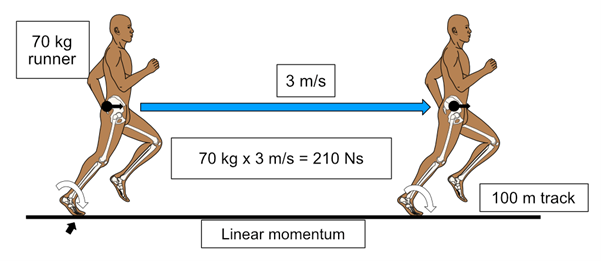
Figure 1. Momentum is mass x velocity, which is easily calculated here to be 210 Newtons per second (Ns). Velocity is displacement over time, so running in a circle back to your start position would create zero velocity and a momentum of only 70 Ns. (Permission wwww.healthystep.co.uk)
In angular momentum, the distance the object is from the axis of rotation is just as important as the size of mass and the velocity. The further from the axis that the mass is, the greater the force required to start or stop it moving as demonstrated in Fig. 2.
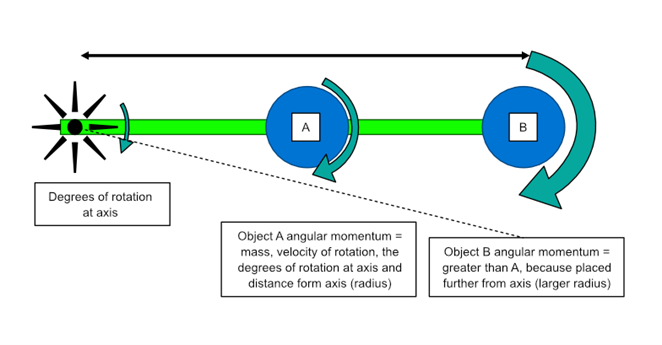
Figure 2. How far an accelerating mass is from the point of rotation affects the size of the moment as well as the size of the mass. Objects A and B are considered equal in mass and are rotating at the same speed, but extra distance gives object B greater angular momentum. (Permission www.healthystep.co.uk).
Moments
Moments are the angular rotational forces associated with angular momentum.
Motion in large joints usually consists of rotations that are dominant in the sagittal plane, known as extension (dorsiflexion) and flexion (plantarflexion). Therefore, the muscles that produce these motions provide extension and flexion moments. In reality, these motions are usually co-existing with smaller frontal and transverse plane moments as well as sliding displacements. Certain joints, such as the hip, offer large amounts of supplementary frontal and transverse plane motions but severely restrict any sliding displacement. The knee and ankle are far more limited in motion outside the sagittal plane but do express significant sliding displacement. However, for simplicity, let us consider that the quadriceps muscles produce extension moments alone at the knee to swing the mass of the lower leg and foot forward, ready for heel strike. Adding heavy boots will move the centre of mass (CoM) of the lower leg further from the knee, requiring greater extension moments from the quadriceps during swing phase. See Fig. 3.
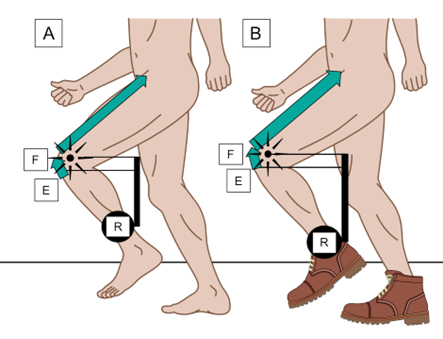
Figure 3. During late swing phase (A) the quadriceps muscles provide effort force (E) at the tibial tuberosity, creating extension moments across the knee. The knee is acting as an axis or fulcrum (F) to move the resistance (R) of the lower leg mass around. The placement of mass within a limb matters, as it affects the position of the CoM being moved during locomotion. Adding heavy boots (B) increases stresses on the quadriceps and patellar ligament during swing phase as a result of larger moments being generated on a larger, more distantly placed resistance. (Permission www.healthystep.co.uk).
Torsions are moments (rotational forces) that are applied through the material of an object in opposite directions or at different rates in different areas. With torsion, the material furthest from the axis of rotation experiences the greatest forces, as shown in Fig. 4. With the foot being fixed to the ground in closed chain, torsions between the distal and proximal parts of anatomy within the pelvis, lower limb and across the foot are common and require restriction.
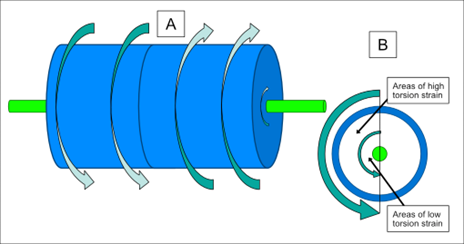
Figure 4. Torsion is a particularly destructive force in biology. It occurs when part of the anatomy rotates in the opposite direction or at a faster rate to the rest of it (A). Tissue further from the axis of torque is under the most stress (B). Such concepts help explain why long bones are able to be almost hollow in the middle but require thick cortical shafts. (Permission www.healthystep.co.uk)
Ground reaction force (GRF)
GRF is easily explained under Newton’s third law which states that ‘every action has an equal and opposite reaction’. When the foot hits the ground the ground pushes back. Thus, the GRF always pushes in the opposite direction to the force derived from the body acting against it. If the ground is hard, it will push back without any deformation, forcing the foot/footwear to do all the shape changes instead.
Forces in gait are highest in the vertical direction because the CoM of the body rises and falls with changes in the functional leg length under muscle power and gravity. The amount of force at any moment is primarily influenced by the gait speed, the mass of the individual, and whether the CoM of the body is rising or falling.
Forces are also driven anteriorly into the ground by the foot at heel strike because the body is falling forward behind the contact limb. Until body mass has passed to a position directly above the foot, the GRF is applied in a posterior direction acting against the body’s own anteriorly directed force. This sagittal plane force decreases until it becomes zero at ‘absolute midstance’ when the body’s CoM is placed vertically over the support limb. Once the mass of the body moves anterior to the ankle, forces are driven posteriorly against the ground, creating anteriorly directed GRFs. Peaks of posterior GRF occur before forefoot loading and anterior GRF forces are greatest during early acceleration after heel lift. Medial-lateral forces are usually very small and far more variable on each step than those in the vertical and sagittal planes. See Fig. 5.
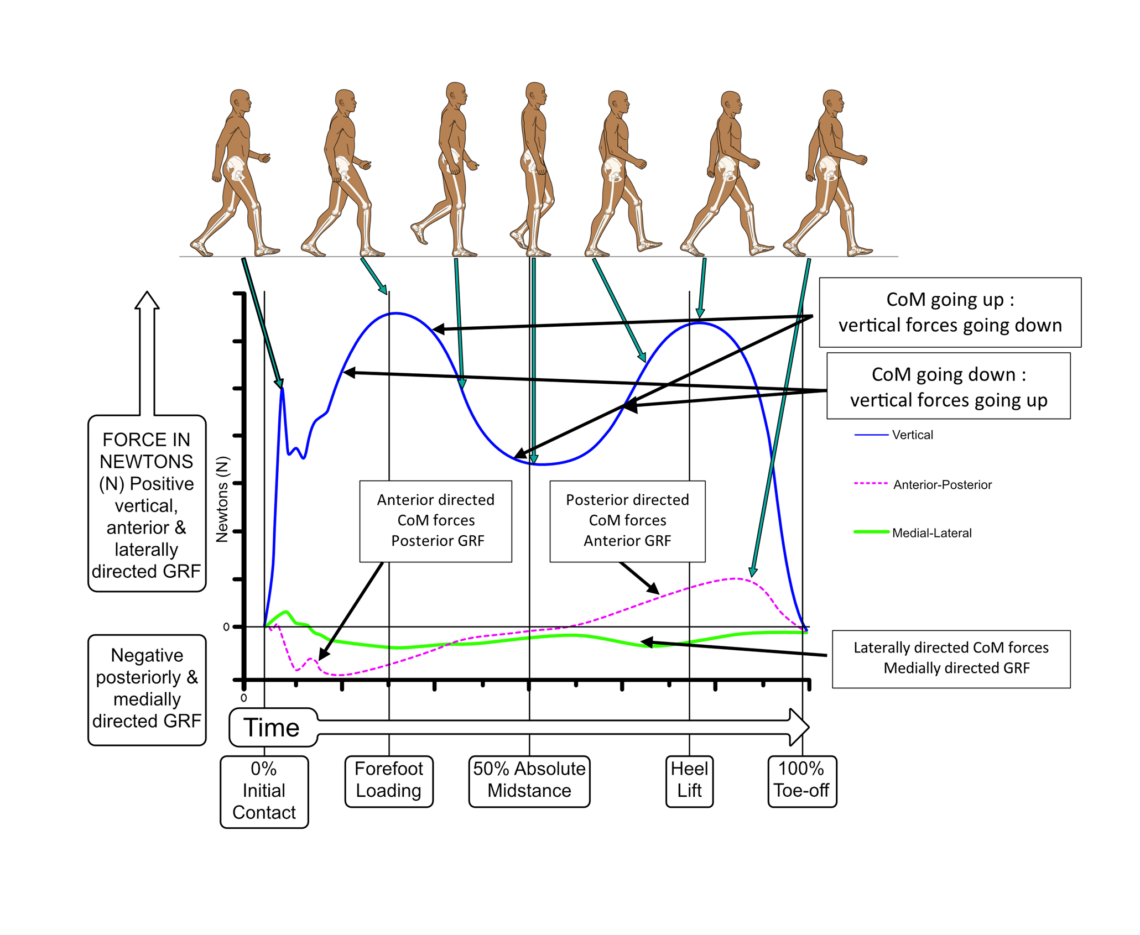 Figure 5. Forces become visible during gait through recording the changes in the ground reaction forces via a force plate. Changes in these forces over time are known as impulses. These impulses are a result of the motions of the body’s CoM and changes in limb positions. (Permission www.healthystep.co.uk)
Figure 5. Forces become visible during gait through recording the changes in the ground reaction forces via a force plate. Changes in these forces over time are known as impulses. These impulses are a result of the motions of the body’s CoM and changes in limb positions. (Permission www.healthystep.co.uk)
Stress
Stress is force over cross-sectional area. This is why tissue diameters within a specific bone or tendon can give an idea of how much strength they offer to resist loads. Thus, a healthy femur requires more force to fracture than a 5th metatarsal and the Achilles can manage much higher tensile forces than can the tendon of tibialis posterior. It also explains the varying shape of anatomical structures, indicating why the enthesis often sees cross-sectional areas of tendons expand before they attach to bone. Stress is a vector because its direction is very important to its meaning. Tension is a positive stress that pulls material away from itself to produce a strain of elongation and width narrowing. Compression is considered a negative stress that pushes material together, changing dimensions by spreading out material away from the load. See Fig. 6.
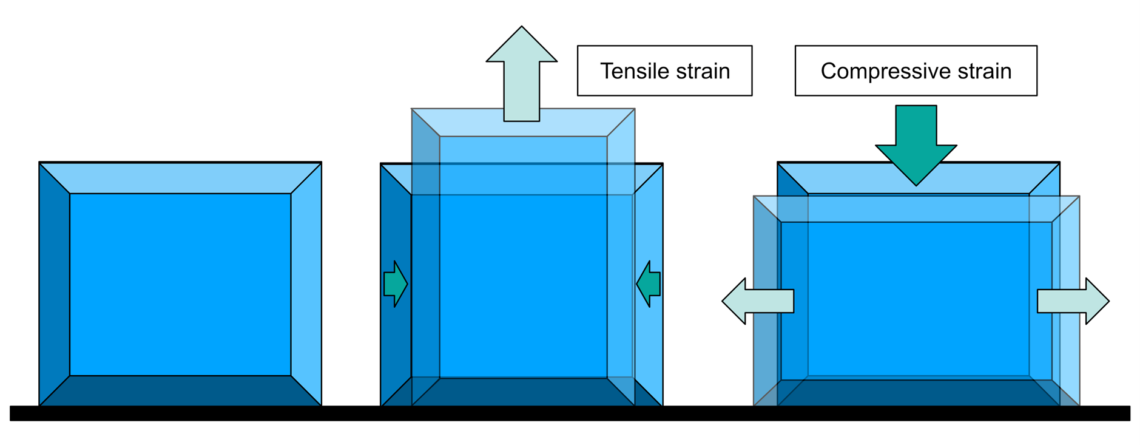
Figure 6. Most solid objects are usually resistant to gravitational stresses but under higher tensional or compressive stress, an object changes its dimensions in a process known as strain. (Permission www.healthystep.co.uk)
Strain
Strain is the proportional change in a material’s dimensions under stress, and again it is positive under tension and negative in compression. This is also a vector because, without direction, we cannot know what is occurring within the material. Under Newtonian mechanics, we expect a material to become longer and narrower under longitudinal tension and wider but shorter under compression, in proportion to the amount of stress. Strain is dependent on the direction of stress and where it is applied, as shown in Fig. 7. However, biological materials express non-Newtonian and non-Hookean properties. Thus, under different amounts and directions of strains, differing loading rates, and quantities of loading cycles, the body’s tissues express dimensional changes differently (Horwood and Chockalingam, 2023b pp.120-123).
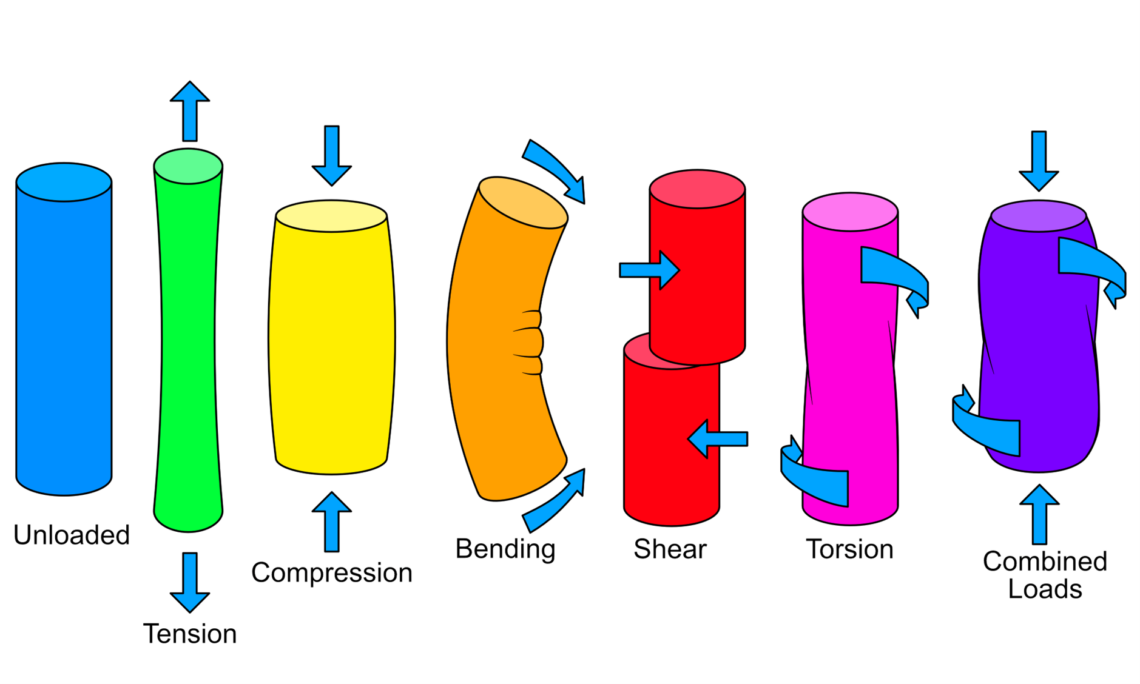
Figure 7. The direction of stress and the resultant strain relate directly to each other, creating a number of types of deformation patterns. These are predictable in most non-organic materials. However, biological tissues are structured in ways to behave variability under different stresses. Most biological structures load with stress in a multitude of directions, but one stress/strain tends to dominate in any given location. Shear and torsion should always be minimised, because they are the most damaging to tissues. (Permission www.healthystep.co.uk)
Pressure
Pressure is a force that is always applied perpendicularly over an area. Force is a vector, but in pressure the direction is known. Area is a scalar as it does not require direction to have meaning. Therefore, pressure is a scalar quantity. With force being equal, the larger the area under force the lower the pressure. This is why relative to body mass, cavoid feet often have areas of higher pressures, whereas flatter profiled feet tend to produce lower peak pressures. Like force, you cannot reduce pressure without altering mass or acceleration. But now, also the size of the surface contact area plays a part in the peak stresses generated.
Claiming that a certain insole reduces pressure can only mean it slows the gait speed down, reduces mass (unlikely), or spreads pressure over a larger surface contact area. Usually, when an insole reduces heel and forefoot pressures, it is because there are increased midfoot pressures via increased contouring under the foot’s central profile. This increases the total plantar pedal contact area that forces are spread over, but this does not change the actual forces generated during locomotion.